
Schraubenberechnung
unter Berücksichtigung der Flankenwinkel, Werkstoffkennwerte und Scherspannungsfaktoren.
von
Dipl.-Ing. Gerhard Friedrich Dose
Goethestraße 47
D 69514 Laudenbach
Tel.: 06201 - 71810
Inhaltsverzeichnis
2.3 Ermittlung der Einschraubtiefen
2.3.1 Mindesteinschraubtiefe für Bolzenbruch
2.3.2 Erforderliche Einschraubtiefe bei Betriebslast
2.3.3 Berechnung der Scherspannungen im Gewinde
2.3.4 Ermittlung des Scherspannungsfaktors
2.4 Berücksichtigung der Toleranzen
2.5 Zulässige Flächenpressung unter den Schraubenköpfen
2.6 Unterschiedliche Gewindearten
2.6.1 Metrisches Gewinde nach DIN 3 und 13
2.6.5 Rundgewinde nach DIN 15403 für Kranhaken
2.6.6 Sägengewinde nach DIN 513, Teil 1 bis 3 (April 1985)
Tabelle 1: PAN-Gleitmetalle
Literatur
Bei der Berechnung von Schraubenverbindungen ging Prof. C. Bach gemäß [1] von der Annahme aus, daß die Gewindegänge im Grunde der Mutter abgebrochen werden. Daraus folgte für ihn, daß die Gewindegänge sowohl auf Biegung als auch auf Schub beansprucht werden. Die größere der beiden Beanspruchungen wurde maßgebend.
In den 50er Jahren wurde statt des Abbrechens ein Abscheren angenommen, wobei jedoch die Höhe des Gewindeganges mit 7/8*P in Ansatz gebracht wurde. Der Versagensdurchmesser wurde mit dem Kerndurchmesser eingesetzt, so daß für die Abscherfläche auch die Anzahl der tragenden Gewindegänge zu berücksichtigen waren.
Bei einer neueren Berechnung, die von Alexander [2] 1977
verfeinert wurde, wurde anscheinend die Theorie von Bach übernommen
und erweitert. Es wird hier davon ausgegangen, daß das Gewinde
entweder im Grunde der Mutter oder des Bolzens abgestreift wird. Die
in [3] im Abschnitt 5.2.2 angegebene Berechnung führt wegen der
nichtstimmigen Annahme des Abstreifens zu unterschiedlichen
Mindesteinschraubtiefen. So wurde, wie in [4] aufgeführt, bei
einer Werkstoffpaarung von 1.4313 für den Bolzen und GGG 40 für
die Mutter die Einschraubtiefen
mB = 0,980*d
für den Bolzen und
mM = 2,326*d für
die Mutter
ermittelt. Bei Versuchen mit diesen Werkstoffen wurde
aber eindeutig festgestellt, daß das Gewinde bei einer
Einschraubtiefe vom m = 1,233*d abgestreift wurde und
bei m = 1,4*d der Bolzen brach.
In einem anderen Fall wurden bei der Werkstoffpaarung 8.8 und St
37 Einschraubtiefen von
mB = 1,848*d für
den Bolzen und
mM = 2,749*d für die
Mutter
errechnet. Im letzteren Fall war die Zugspannung so groß,
daß 90 % der Streckgrenze erreicht wurden.
Zwischenzeitlich wurde 1981 seitens der DDR die TGL 38512 erarbeitet und eingeführt. Die im Abschnitt 4.2.8 auf Seite 11 aufgeführte Formel für die Mindesteinschraubtiefe berücksichtigte zwar keinen Abstreifdurchmesser und keinen Scherspannungsfaktor, erzielte aber nur einen Wert für die Einschraubtiefe.
Abweichend von den Normalfällen ‘Schraube und Mutter’, werden Schraubverbindungen hergestellt, wo der Mutternwerkstoff eine wesentlich geringere Streckgrenze als der Bolzenwerkstoff besitzt. Auch umgekehrt kann das der Fall sein.
Da die Kraft im Bolzengewinde gleich der Kraft im Mutterngewinde ist, ergeben sich für die beanspruchten Scherflächen die Gleichung
At ,B*t B = F = At ,M*t M.
An Hand dieser Gleichung ist ersichtlich, daß bei unterschiedlichen Scherspannungen t B und t M die Scherfläche A desto größer sein muß, desto kleiner der Wert t ist.
Die Berechnung nach [4] folgt der vorstehenden Gleichung, so daß bei absolut gleichen Werkstoffwerten der Abstreifdurchmesser dem Flankendurchmesser entspricht. Bei unterschiedlichen Werkstoffwerten verschiebt sich der Abstreifdurchmesser im ungekehrten Verhältnis der Werkstoffkennwerte, also bei "schlechterer" Mutter nach außen, bzw. bei "besserer" Mutter nach innen.
Bei einer belasteten Schraubverbindung sind die tragenden Gewindegänge auf Biegung und auf Schub beansprucht. Die in der Berechnung eingesetzte Scherspannung ist eine Ersatzspannung für die auftretenden Biege- und Schubspanungen mit
t m,pB,M = b
B,M*Rm,pB,M,
wobei b
B,M die Scherspannungsfaktoren für die Bolzen bzw.
Muttern und für die verschiedenen Werkstoffe unterschiedlich
sind. Diese Werte wurden in weit mehr als 100 Versuchen ermittelt.
Siehe hierzu auch [4, 5 und 6]
In Bild 1 ist links bei dem abgestreiften Gewinde deutlich zu sehen, daß im eingeschraubten Bereich sowohl der Bolzen als auch die Mutter abgestreift wurden. In diesem Fall stimmten der errechnete und der gemessene Abstreifdurchmesser überein. Im allgemeinen wurde jedoch festgestellt, daß hier geringfügige Abweichungen vorhanden sind, wie aus den Versuchsprotokollen in [4, 5 und 6] ersichtlich.

Bild 1: Abgestreiftes Gewinde und gebrochener Bolzen
Die abgebildeten Versuche wurden mit Schraubenbolzen M 20 x 110 in 8.8 und Muttern aus PAN-Bonze 220 gefahren. Es wurde nachstehende Werte ermittelt:
Links: Einschraubtiefe m = 15 mm, Zugkraft F = 224,2 kN Abstreifdurchmesser dt = 18,70 mm
Rechts: Einschraubtiefe m = 17 mm, Zugkraft F =224,2 kN mit Bolzenbruch
Für die Schraubenverbindungen sind zwei Kriterien zu beachten:
1. Um festzustellen, ob bei eine Schraubenverbindung bei einer Überlastung das Gewinde abgestreift wird oder ob der Bolzen bricht, sind für die Materialkennwerte die Zugfestigkeiten zu berücksichtigen. Die ermittelte Mindesteinschraubtiefe ist dann um ca. 5 % zu vergößern. Damit wird sichergestellt, daß bei Überbelastung der Bolzen versagen wird.
2. Bei den allgemeinen Nachweisen, wo eine Sicherheit gegen die Streckgrenze gefordert wird, sind für die Spannungsnachweise und Ermittlung der erforderlichen Einschraubtiefe die Kennwerte der Streckgrenzen zu berücksichtigen.
Die Berechnungsgänge sind in beiden Fällen gleich.
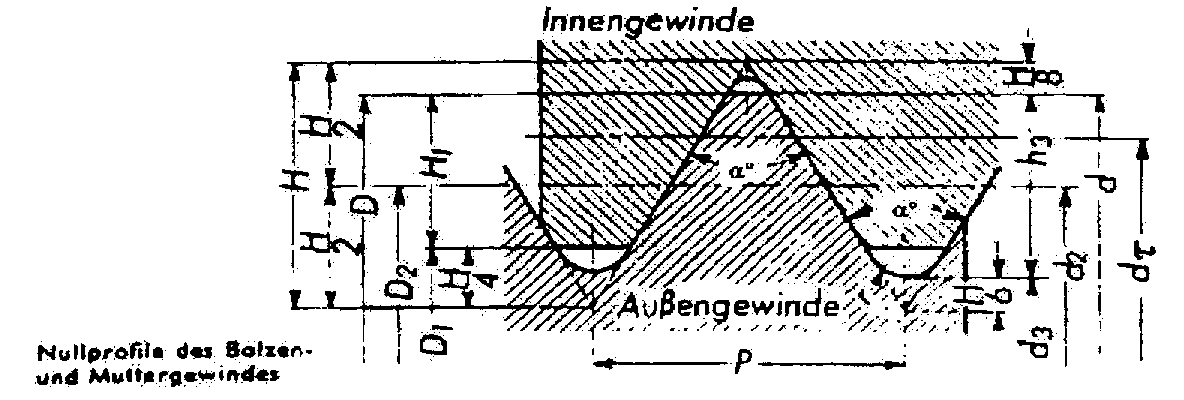
Bild 2: Nullprofil des Bolzen- und Mutterngewindes
Es werden unter Berücksichtigung von Bild 2 folgende Formelzeichen verwendet:
F Äußere oder gesamte Schraubenzugkraft
FV Schraubenvorspannkraft
FBr = RmB*As Schraubenbruchkraft
MA Schraubenanzugsmoment
a B,M Werkstoff-Faktor für Schraube oder Mutter
b B,M Scherspannungsfaktor
a ° Flankenwinkel
RmB,M Zugfestigkeit des Bolzen- oder Mutternwerkstoffes
RpB,M Streckgrenze des Bolzen- oder Mutternwerkstoffes
t mB,M = b B,M*RmB,M Grenz-Scherspannung des Bolzens bzw.der Mutter
t pB,M = b B,M*RpB,M Streckgrenzen-Scherspannung des Bolzens bzw.der Mutter
t B,M,vor vorhandene Scherspannung des Bolzens bzw. der Mutter
d, d2 Gewindedurchmesser, Flankendurchmesser des Gewindes
dt , m Durchmesser des Abscherzylinders, tragende Gewindelänge
As Spannungsquerschnitt des Bolzens
At Gesamtfläche des Abscherzylinders
At B,M Scherfläche des Bolzen- bzw. Mutterngewindes
P, H Gewindesteigung, Höhe des Grunddreiecks
2.3 Ermittlung der Einschraubtiefen
Bei den vorstehend genannten Versuchen wurde auch festgestellt, daß bei einer geringen Dehnung des Mutternwerkstoffes, Dehnung A < 4 %, bei gleichen, bzw. fast gleichen Zugkräften die Gewindegänge am Bolzen und Mutter nicht abgestreift wurden, sondern daß die Mutter, wie in Bild 3 zu sehen, kugelpfannenförmig platzte. Dieses wurde sowohl bei der hier abgebildeten PAN-Bronze 16, als auch bei GG und Alminiumguß festgestellt.

Bild 3: Kugelpfannenförmig geplatzte Mutter PAN 16 mit Bolzen M 20 x 110 aus 5.6
Links:Einschraubtiefe m = 17 mm, Zugkraft F =
135, 6 kN, Mutter geplatzt
Rechts: Einschraubtiefe m =
19 mm, Zugkraft F = 135,8 kN mit Bolzenbruch
Anmerkung: Es hat sich herausgestellt, daß bei bestimmten Werkstoffkombinationen die erforderliche Einschraubtiefe kleiner sein kann als die Mindesteinschraubtiefe. Aus diesem Grunde sollten beide Fälle durchgerechnte werden.
2.3.1 Mindesteinschraubtiefe für Bolzenbruch
Hierfür sind die Zugfestigkeiten der Werkstoffe einzusetzen. Unter der Annahme,. daß die Scherspanungsfaktoren nicht gleich sind, ergibt sich folgender Berechnungsgang:
Unter Berücksichtigung der zul. Scherspannungen ist zuerst der Abstreifdurchmesser zu ermitteln. Die zul. Scherspannungen errechnen sich für den Bolzen und die Mutter
t mB = b B*RmB
t mM = b M*RmM.
Aus dem umgekehrten Verhältnis der zul. Scherspannungen ergeben sich die Werkstoff-Faktoren für den Bolzen und die Mutter zu
a B = t mM/(t mM+t mB)
a M = 1-a B.
In der Mitte des theoretischen Gewindes liegt der Flankendurchmesser d2 zwischen den Gewindespitzen. Das Maß vom Flankendurchmesser d2 bis zur Gewindespitze beträgt H/2. Bei den unterschiedlichen Werkstroffkennwerten, wie Zugfestigkeit bzw Streckgrenze, verschiebt sich der halbe Durchmesser um den Wert
D d/2 = H/2-HB/2
wobei HB = a B*P/tan (a °/2) ist.
Unter Einbeziehung des Flankendurchmesser d2, dem Wert 05 = tan (g °/2)*H/P und dem Faktor a B beträgt der Abstreifdurchmesser
dt = d2 + (0,5-a B)*P/tan (a°/2),
Da hier die Steigung eingeht, ergeben sich für das Regel- und das Feingewinde unterschiedliche Einschraubtiefen.
Die Bruchkraft des Bolzens beträgt
FBr = RmB*As.
Mit dieser Kraft errechnet sich die erforderliche Scherfläche des Abscherzylinders zu
At = FBr*(1/t mM+1/t mB)
Unter Berücksichtigung des Abstreifdurchmessers beträgt dann die Mindesteinschraubtiefe
mmin = At /(dt *p )
Bei dieser Einschraubtiefe herrscht "Gleichgewicht" zwischen den tragenden Gewindegängen und dem Spannungsquerschnitt des Bolzens. Um ein Abstreifen sicher zu verhindern muß die Mindesteinschraubtiefe etwas erhöht werden. Es wird eine Erhöhung von ca. 5 % empfohlen.
2.3.2 Erforderliche Einschraubtiefe bei Betriebslast
Bei geforderten Sicherheiten zur Streckgrenze kann die Sicherheit nicht nur darin bestehen, daß die geforderte Sicherheit im Spannungsquerschnitt des Bolzens vorhanden ist, sondern es sollte selbstredend sein, daß dieselbe Sicherheit auch in den Gewindegängen, also bei einem Sack- oder Gewindedurchgangsloch vorhanden sind. Da sich bei der Sicherheit die zulässsigen Spannungen proportional verhalten, kann die erforderliche Einschraubtiefe mit der Zugkraft an der Streckgrenze und den Mindestwerten der Streckgrenzen errechnet werden.
Es betragen die Zugkraft an der Streckgrenze
Fp = As*Rp
und die Scherspannungen des Bolzens und der Mutter
t pB = b B*RpB
t pM = b M*RpM.
Mit diesen Werten errechnen sich die Werkstoff-Faktoren für den Bolzen und die Mutter zu
a B = t pM/(t pM+t pB)
a M = 1-a B
und der Abstreifdurchmesser
dt = d2+(0,5-a B)*P/tan (a°/2).
Die Scherfläche des Abscherzylinders ist dann
At = Fp*(1/t pM+1/t pB)
Mit dem Abstreifdurchmesser dt errechnet sich die erforderliche Einschraubtiefe zu
merf = At /(dt *p ).
Die bisher bekannten Scherspannungsfaktoren sind in den Tabellen des Programms SR 1 enthalten. Sollte ein Werkstoff verwendet werden, von dem der Scherspannungsfaktor b M noch nicht bekannt ist, sollte konservativ b M = 0,5, bei Knetaluminium b M = 0,4 eingesetzt werden, sofern der Scherspannungsfaktor nicht gemäß Abschnitt 2.3.4 ermittelt werden kann.
2.3.3 Berechnung der Scherspannungen im Gewinde
Um bei einer bestehenden Schraubenverbindung die vorhandenen Scherspannungen bei der Betriebskraft der Schraube und die vorhandene Sicherheit zu ermitteln, ist zuerst mit den Scherspannungen der Werkstoffkennwerte der Werkstoff-Faktor
a B = t pM/(t pM+t pB)
a M = 1-a B
und damit der Abstreifdurchmesser
dt = d2 + (0,5-a B)*P/tan (a /2°)
zu ermitteln.
Damit errechnet sich die Scherfläche des Abscherzylinders zu
At = dt *p *m
Dieser Wert teilt sich nun im Verhältnis der
Werkstoff-Faktoren in den Anteil des Bolzens und der Mutter mit
At
B = At *a
B A
t M = At *a M
Damit lassen sich die Einzelscherspannungen für das Bolzen- und Mutterngewinde errechnen.
t B,vor = F/At B
t M,vor = F/At M.
Die Sicherheiten ergeben sich damit für die Schraube und Mutter zu
n B = t pB/t B,vor
n M = t pM/t M,vor.
Es sollte n B = n M > 1,5 sein.
2.3.4 Ermittlung des Scherspannungsfaktors b B,M
Es ist für die Berechnung des Faktors zwingend erforderlich, Versuche zu machen, da die Gestaltsänderungshypothese nach von Mises nicht immer zutreffend ist, wie auch aus den Tabellen im Programm SR 1 ersichtlich. Davon ausgehend, daß der Faktor für den Mutternwerkstoff nicht bekannt ist, müssen für die Versuchsstücke die Zugfestigkeitswerte ermittelt werden. Mit einem Bolzengewinde, von dessen Werkstoff der Faktor bekannt ist, wird dann eine Zugprobe zur Bestimmung der Zugfestigkeit und der Bruchkraft gemacht. Zur Vorschätzung der Einschraubtiefe wird für den Mutternwerkstoff angenommen, daß der Faktor b M » 0,58 beträgt. Mit den Formeln im Abschnitt 2.3.1 wird die Einschraubtiefe errechnet. Bei dem Versuch wird entweder das Gewinde abgestreift oder der Bolzen bricht. Bei einem abgestreiften Gewinde sind die Abstreifdurchmesser sowohl am Gewindeloch als auch beim Bolzen zu messen. Mit den bei dem Versuch festgestellten Werten der Zugkraft, dem Mittelwert der gemessenen Abstreifdurchmesser und der tragenden Einschraubtiefe kann nun der ungefähre Scherspannungsfaktor für den Mutternwerkstoff errechnet werden.
Mit den Meßergebnissen wird die Gesamtfläche des
Abscherzylinders berechnet
At =
m*dt *p
Aus der beim Abstreifen festgestellten Abstreifkraft wird die "rechnerische Scherspannung" für den Bolzen ermittelt:
t mB = b B*F/As, wobei bekannte b B im Programm SR 1 aufgelistet sind.
Mit diesem Wert kann nun die "rechnerische Scherspannung" der Mutter errechnet werden:
t mM = (At /F-1/t mB)-1
Damit ergibt sich der Scherspannungsfaktor zu
b M = t mM/RmM
Mit diesem Wert muß mit der Bruchkraft des Bolzens eine Kontrollrechnung gemäß den Formeln in Abschnitt 2.3.1 durchgeführt werden, um mit weiteren Versuchen die Einschraubtiefe beim Bolzenbruch zu ermitteln. Wie die Versuchsergebnisse in [5] zeigen, können unter günstigsten Umständen bereits 2 Versuche ausreichend sein.
Es muß aber ausdrücklich darauf hingewiesen werden, daß der Scherspannungsfaktor zu ungenau ist, wenn der Abstand von der Bruchkraft zur Abstreifkraft groß ist. Aus diesem Grunde sollten bei zwei Versuchen die Einschraubtiefen und die festgestellten Kräfte dicht beieinander liegen und bei der größeren Kraft der Bolzenbruch erfolgt sein.

Bild 4: Austenitischer Bolzen A2-70, M 16 mit Alumutter aus 3.0615.71 (F 28)
Einschraubtiefe: m = 21 mm, Längung: 25 mm, Bruchkraft: F = 128 kN
Ferner muß auch darauf hingewiesen werden, daß bei austenitischen Schraubenbolzen mit gerolltem Gewinde der Bolzenbruch nicht im Spannungsquerschnitt des Gewindes, sondern im Schaftteil erfolgt, wie in Bild 4 zu sehen ist. Dies ist auf eine Werkstoffverfestigung beim Gewinderollen zurück zu führen.
Zur Berechnung der Einschraubtiefe muß trotz des Bruches im
Schaft mit dem Spannungsquerschnitt im Gewinde gerechnet werden, also
mit
F = Rm*As.
Sollte statt des Mutternwerkstoffes der Scherspannungsfaktor des Bolzens ermittelt werden, so ist sinngemäß mit den entsprechenden Werten zu verfahren.
2.4 Berücksichtigung der Toleranzen
Die Gewinde werden nicht immer in den üblichen Toleranzen 6H/6g hergestellt, sondern auch mit größeren Abmaßen. Hier ist zu beachten, daß die Einschraubtiefe um den Betrag vergrößert wird, der sich aus den Toleranzmaßen ergibt. Erfahrunsggemäß sind diese Maße nicht besonders groß, so daß bei einer Erhöhung der rechnerischen Einschraublänge um ca. 5 % solche Abmaße kompensiert sein können..
Eine andere als sie übliche Toleranz hat keinerlei Einfluß auf das Maß des Abstreifdurchmessers. Unter der Annahme, daß der Kraftangriff im Abstreifdurchmesser erfolgt, kann davon ausgegangen werden, daß die in den Gewindegängen auftretenden Biegebeanspruchungen sich auch nicht anders verhalten, als wenn die übliche Toleranz vorhanden sei.
Bei einem rechnerischen Nachweis sind die entsprechenden Toleranztabellen der Normen zu berücksichtigen, wie sie beispielsweise für das metrische ISO Regelgewinde in der DIN 13, Teil 20 und für das Feingewinde in DIN 13, Teil 21 aufgeführt werden.
2.5 Zulässige Flächenpressung unter den Schraubenköpfen
Im Rahmen einer Dissertation wurden an der TU Darmstadt Untersuchungen durchgeführt, um die zulässige Flächenpressung unter dem Schraubenkopf und der Mutter zu ermitteln. In [7] wurden die Ergebnisse dargestellt
Danach sind die zulässigen Flächenpressungen abhängig von der Brinellhärte des Werkstoffes. Unabhängig von den Legierungen, also auch bei Grauguß, austenitische und martensitische Stählen wird die vorhandene oder Mindest- Brinellhärte mittels der Tabelle in DIN 50150 in die "rechnerische Zugfestigkeit" umgerechnet. Der so ermittelte Wert pG liegt nach [7] unterhalb des Wertes pG,0,025 mm, bei dem eine bleibende Verformung von 25 µm eintritt. Da bei den ferritschen Stählen ein fester Bezug HB zu Rm besteht, kann somit für diese Stähle pG = Rm gesetzt werden. Die auf vorstehender Basis ermittelten zulässigen Flächenpressungen pG sind in den Werksofftabellen des Programms SR 1 mit aufgeführt.
Die Flächenpressung errrechnet sich nach Junker mit den
Formelzeichen
Fmax = Maximale Kraft des
Schraubenbolzens
(FM+F *FA,, wobei F = FSA/FA nach VDI 2230)
dw = Auflagen-Außendurchmesser des
Bolzenkopfes oder Mutter
da =
Auflagen-Innendurchmesser der Bohrung, eventuell einschließlich
Aussenkung.
Die auftretende Flächenpressung beträgt mit der Auflagerfläche
Ap = (dw²-da)*p
/4
pvorh = Fmax/Ap
£ pG.
Sollte die Flächenpressung zu hoch sein, so kann mittels
einer Unterlegscheibe mit entsprechender Zugfestigkeit die
Auflagerfläche vergrößert werden. Der
Außendurchmesser vergrößert sich damit auf
dw’
= dw+2s
wobei s die Dicke der
Unterlegscheibe ist. Sollte dieses Maß größer sein
als der Außendurchmesser der Scheibe, so ist das kleinere Maß
zu berücksichtigen.
2.6 Unterschiedliche Gewindearten
Bei den unterschiedlichen Gewindearten ändert sich nur die Formel für den Abstreifdurchmesser, da hier der halbe Flankenwinkel einzusetzen ist. Die weiteren Berechnungsschritte, wie vorstehend aufgeführt, ändern sich nicht.
Bei dem Trapez-, Rund- und Sägengewinde wird zusätzlich auf die abweichende tragende Fläche der Gänge hingewiesen.
2.6.1 Metrisches Gewinde nach DIN 3 und 13
Bei dem metrischen Gewinden beträgt der Flankenwinkel a
= 60 °. Da hier die Höhe des Grunddreiecks
H =
0,86603*P beträgt, wird der Zahlenwert 0,86603*tan 30°
= 0.5. Somit lautet die Formel für den Abstreifdruchmesser
dt
= d2 + (0,5-a
B)*P/tan 30°.
Whitworth-Gewinde, wie das Regel-, das Fein- und auch das
Rohrgewinde haben einen Flankenwinkel von
g
= 55°, sofern sie nicht auf einen Flankenwinkel von a
= 60° umgestellt sind. Da die Höhe des Grunddreiecks hier
H = 0,960491*P
beträgt, beträgt der zu betrachtenden Zahlenwert 0,960491*tan 27,5° = 0,5. Unter Berücksichtigung des Flankendurchmesser d2 lautet somit die Formel für den Abstreifdurchmesser
dt = d2+(0,5-a B)*P/tan 27,5°.
Das Panzergewinde hat einen Flankenwinkel von a = 80° mit einer Höhe des Grunddreiecks von
H = 0,595875*P.
Daraus ergibt sich der Zahlenwert zu 0,595875*tan 40° = 0,5. Somit lautet die Formel hier unter Berücksichtigung des Flankendurchmessers
dt = d2+(0,5-a B)*P/tan 40°.
2.6.4 Trapezgewinde nach DIN 103
Trapezgewinde werden bekanntlich vorwiegend bei Spindeln eingesetzt. Wenn auch in der DIN 103, Teil 3, Tabelle 3 Einschraublängenbereiche in den Gruppen N und L vorgeschlagen und in Tabelle 9 die entsprechenden Toleranzfelder genannt werden, werden die zulässigen Flächenpressungen, bei denen noch eine Gleitbewegung möglich ist, voraussichtlich überwiegend maßgebend sein. Trotzdem sollte bei der Materialpaarung darauf geachtet werden, daß der Abstreifdurchmesser innerhalb der tragenden Gewindeflanken liegt.
Mit dem Flankenwinkel von a = 30° für das Trapezgewinde und einer Höhe des Grunddreiecks von
H = 1,866*P
beträgt der Zahlenwert 1,866*tan 15° = 0,5. Damit lautet die Formel für den Abstreifdurchmesser unter Berücksichtigung des Flankendurchmessers
dt = d2+(0,5-a B)*P/tan 15°.
Aus der DIN 103, Teil 1 (siehe Bild 2 und Bild 3) geht hervor, daß
die Gewindetiefe des Grundprofils
H1 = 0,5P
beträgt. UnterBerücksichtigung der tragenden Höhe
ergibt sich als maximaler Abstreifdruchmesser
dt = d2+H1 = d2+0,5P
Da der Wert (0,5-a B)*P/tan 15° = 0,5P ist ergibt sich der maximale Werkstoff-Faktor zu
a B = 0,5-0,5*tan 15° = 0,366
für den größten Abstreifdurchmesser. Beim kleinsten Abstreifdurchmesser beträgt
a B = 1-0,366 = 0,634
Mit diesen Werten würden die Abstreifdurchmesser bei den Gewindespitzen des Bolzens und der Mutter liegen.
Um sicher zu stellen, daß der Abstreifdurchmesser nicht an den Spitzen der Gewindegänge liegt, sollte die Bedingung
d > dt > D1
erfüllt sein. Diese Bedingung ist dann erfüllt, wenn der Werkstoff-Faktor
a B = 0,375 bis 0,625
beziehungsweise, wenn das Verhältnis der Scherspannungen
t pM/t pB = 3/5 bis 5/3
beträgt. Das würde einer tragenden Flankenhöhe von 0,467P entsprechen.
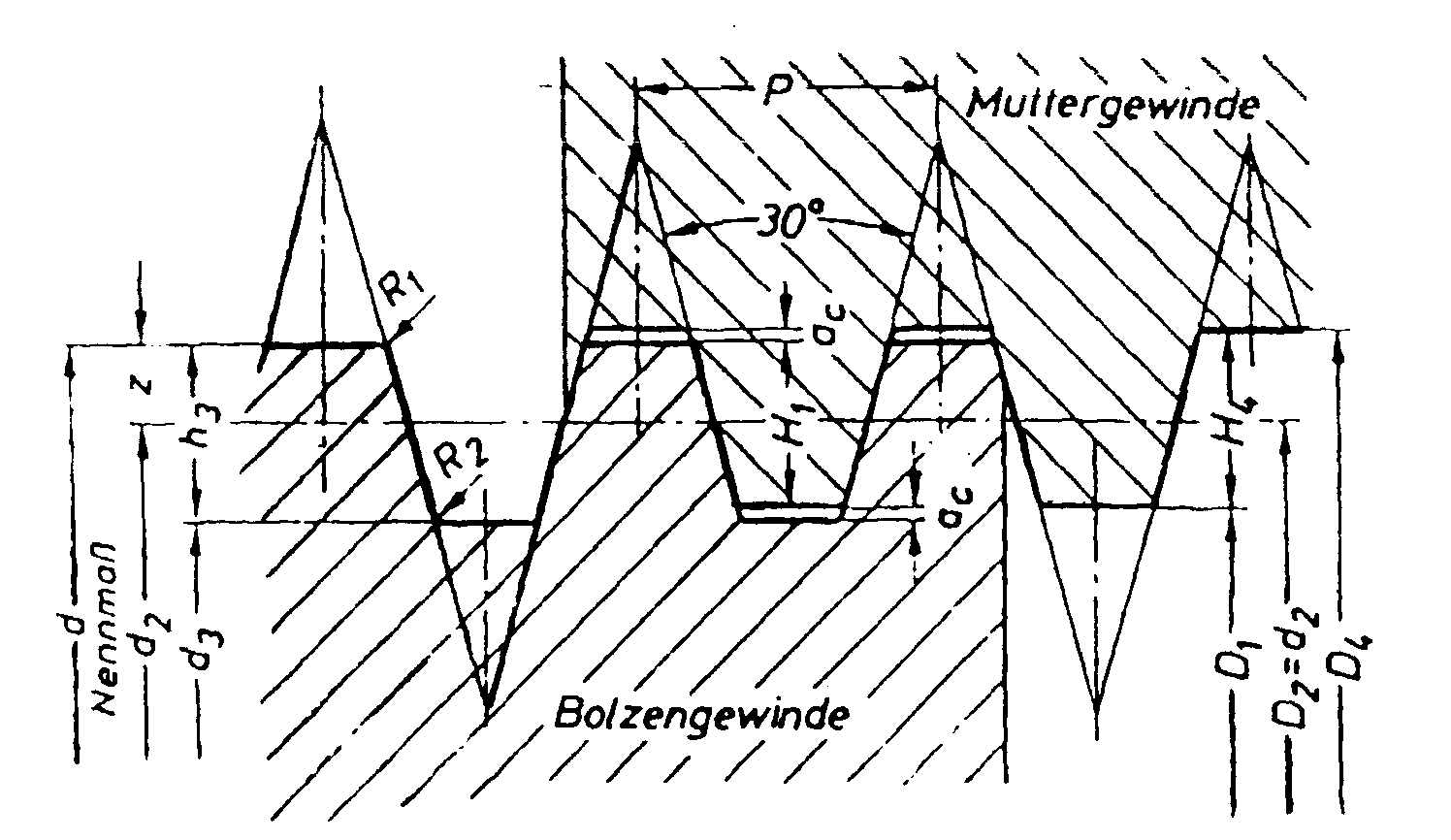
Bild 5: Profile für Bolzen und Mutterngewinde
Zusätzlich zu den Formelzeichen bei Bild 2 sind noch folgendes Formelzeichen zu beachten:
D1 [mm] Kerndurchmesser des Mutterngewindes
P [mm] Steigung des eingängigen und Teilung des mehrgängigen Gewindes
Fs [N] Betriebskraft der Spindel
AK [mm²] Kernquerschnitt der Spindel
Apw [mm²] Fläche für Flächenpressung pro Windung
Ap,erf [mm²] Erforderliche Fläche für Pressung
werf [--] erforderliche Windungen bei Pressung
mw [--] erforderliche Mutternhöhe aus Pressung
s [mm] Flankenspiel
Zur Berechnung der Werkstoffpaarung wird von der Spindel ausgegangen. Mit den Daten für die Spindel wird als erstes die Kraft an der Streckgrenze
FpB = Fs*n
ermittelt, wobei Fs die Betriebskraft und n die geforderte Sicherheit ist.
Wenn die Daten der Spindel bekannt sind, so ergibt sich mit dem Kernquerschnitt
AK = d3²*p /4
die erforderliche Streckgrenze des Bolzenwerkstoffes zu
RpB = FpB/AK.
so daß damit der Werkstoff für die Spindel bestimmt werden kann.
Ist jedoch der Werkstoff vorgegeben, so errechnet sich der Kernquerschnitt zu
AK = FpB/ RpB,
so daß damit die Spindeldaten bestimmt werden können.
Zur Ermittlung des Mutternwerkstoffes ist das Verhältnis der Scherspannungen zu beachten. Damit ergibt sich die Streckgrenze des Mutternwerkstoffes zu
RpM = RpB*b B*3/(5*b M) bis RpB*b B*5/(3*b M)
Da bei einigen Bronze-Werkstoffen auch die zulässige Flächenpressungbei der Gleitbewegung angegeben wird, kann nunmehr die Mindestanzahl der Windungen aus der Betriebkraft berechnet werden. Die erforderlich Fläche beträgt
Ap,erf = Fs/pzul
Mit der Fläche pro Windung
Apw = d2*p *P/2
ergibt sich die erforderliche Anzahl der Windungen zu
werf = Ap,erf/Apw,.
Damit wird die erforderliche Mutternhöhe aus der Flächenpressung
mw = werf*P
errechnet.
Die Berechnung der erforderlichen Mutternhöhe unter Berücksichtigung der Sicherheiten erfolgt wie im Abschnitt 2.3.3 angeführt Die jeweils größere Mutternhöhe ist dann für die Konstruktionsausführung maßgebend.
Wie in Bild 6 ersichtlich, werden auch Trapezgewinde mit Flankenspiel hergestellt. Auch hier beträgt der Abstreifdurchmesser
dt = d2+(0,5-a B)*P/tan 15°
Für die Ermittlung der erforderlichen Einschraubtiefe sind die vorhandenen Flankenspiele zu berücksichtigen, wobei die Grenzmaße für die Muttergewinde der DIN 103, Blatt 5 und Blatt 6 und für das Bolzengewinde den Blättern 7 und 8 zu entnehmen sind.
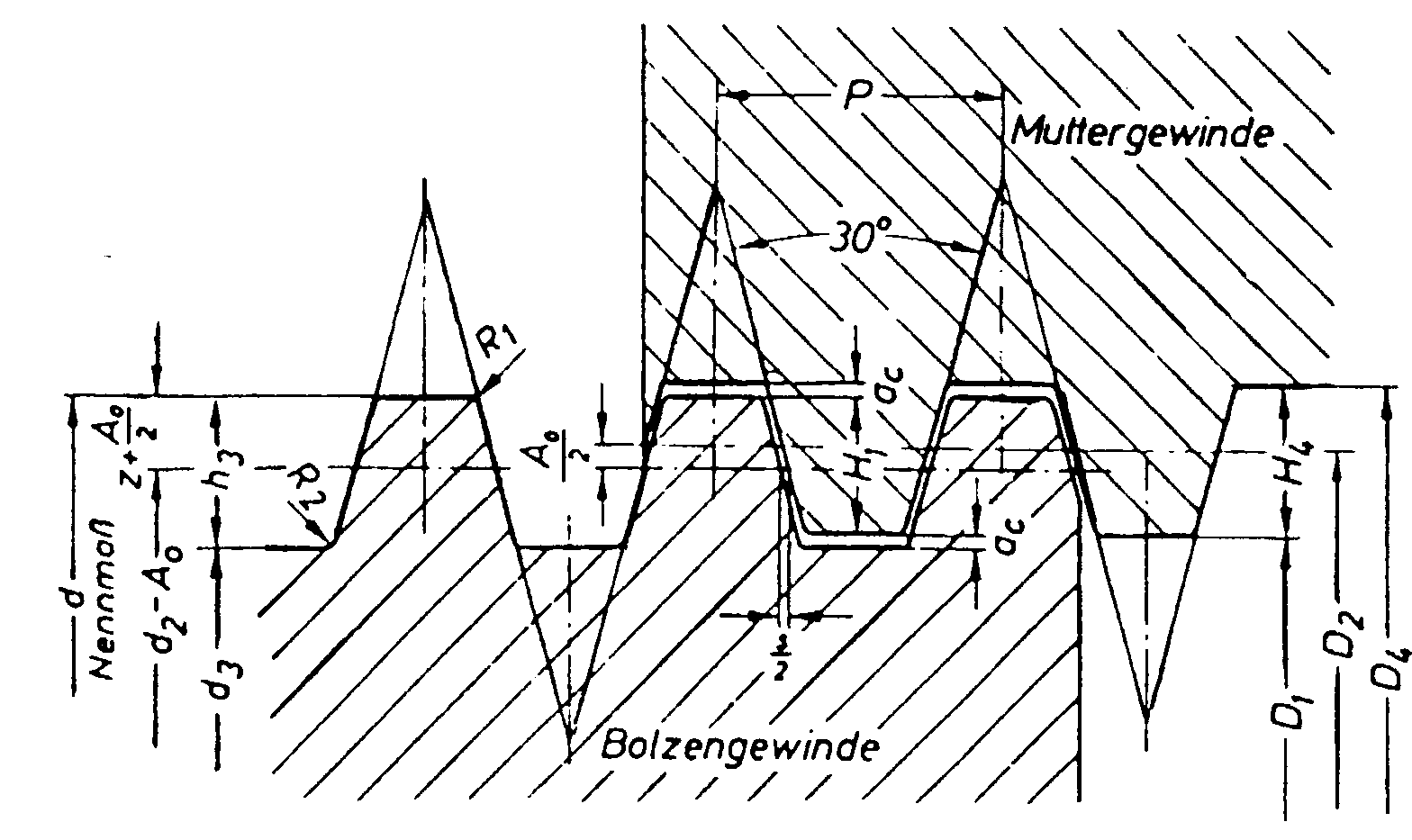
Bild 6: Profil mit Flankenspiel
Die erforderliche Einschraublänge vergrößert sich um das Maß, das sich aus der Anzahl der Steigungen und dem doppelten Toleranzmaß s/2 ergibt.
2.6.5 Rundgewinde nach DIN 15403 für Krankaken
Achtung: Die Bezeichnungen beim Rundgewinde weichen von den üblichen Formelzeichen ab! Die Formelzeichen beziehen sich auf die Angaben in Bild 7.
Wie bei den vorherigen Gewinden ist beträgt beim Rundgewinde
mit einem Flankenwinkel von a = 30°
und einer Höhe des Grunddreiecks von
t = 1,866*h
der Zahlenwert 1,866*tan 15° = 0,5.
Bei dem Rundgewinde beträgt der Flankenwinkel der kurzen tragenden Flanke, wie bei den meisten Gewinden, a = 30°. Damit lautet die Formel für den Abstreifdurchmesser
dt = d2+(0,5-a B)*P/tan 15°
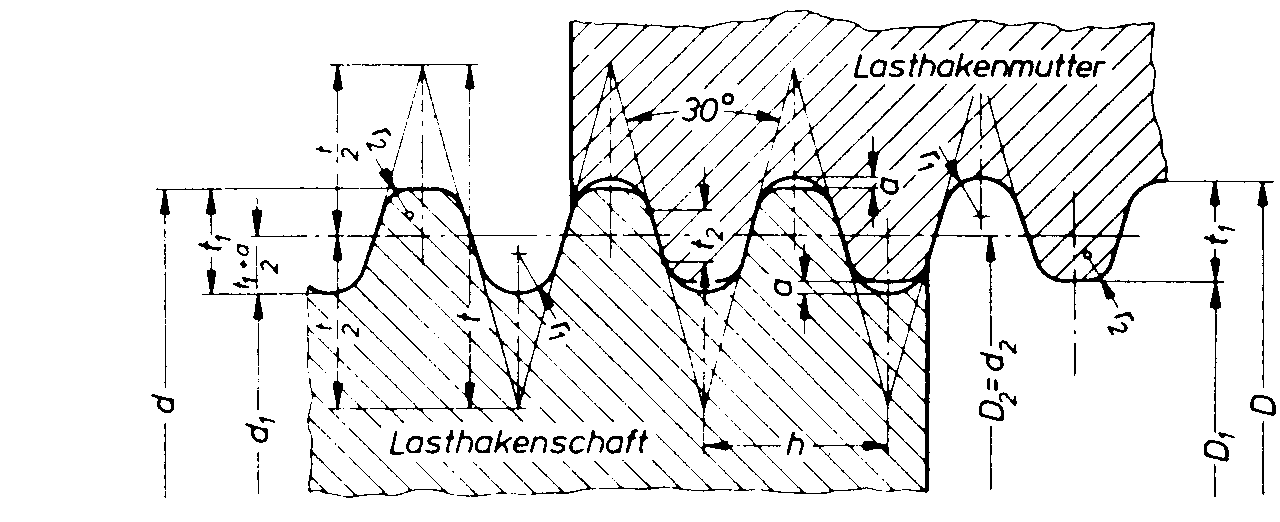
Bild 7: Rundgewinde nach DIN 15403
Es sind noch folgende technische Daten zu beachten:
Gewindesteigung h » d/9
Tiefe des Gewindedreiecks t = 1,866*h
Gewindetiefe t1 =0,55*h
Tragende Flankentiefe t2 = 0,27234*h
Freiheit Gewindekopf/Ausrundung a = 0,05*h
Radius am Gewindegrund r1 = 0,22104*h
Radius an der Gewindespitze r2 = 0,15359*h
Wie schon beim Trapezgewinde aufgezeigt, darf der Abstreifdurchmesser nicht außerhalb der tragenden Flankenfläche liegen. Daraus ergibt sich mit t2 = (0,5-a B)*h/tan 15° = 0,27234*h für den größten Abstreifdurchmesser der Werkstoff-Faktor zu
a B = 0,5-0,27234*tan 15° = 0,427
und für den kleinsten Abstreifdurchmesser
a B = 1-0,427 = 0,573.
Da hier die Auflagefläche nicht an den Gewindespitzen enden, ist es nicht erforderlich den Auflagebereich zu verkleiner.
Die weiteren Berechnungen der Einschraubtiefe, der Scherspannungen und der Sicherheiten erfolgt wie im Abschnitt 2.3.3 aufgeführt.
2.6.6 Sägengewinde nach DIN 513, Teil 1 bis 3 (April 1985)
Das Sägengewinde wird, wie auch das Trapezgewinde, vorwiegend als Bewegungsschraube eingesetzt. Es hat gegenüber dem Trapezgewinde den Vorteil, daß die Radialkräfte aus der Flächenpressung bei einen Flankenwinkel von 3° wesentlich kleiner werden, als bei dem Trapezgewinde mit einen Winkel von 15° für die tragenden Flanken.
Aus meßtechnischen Gründen mußte für die Höhe des Grunddreicks sowohl der nichttragende Flankenwinkel von 30° als auch der tragende Flankenwinkel von 3°berücksichtigt werden.
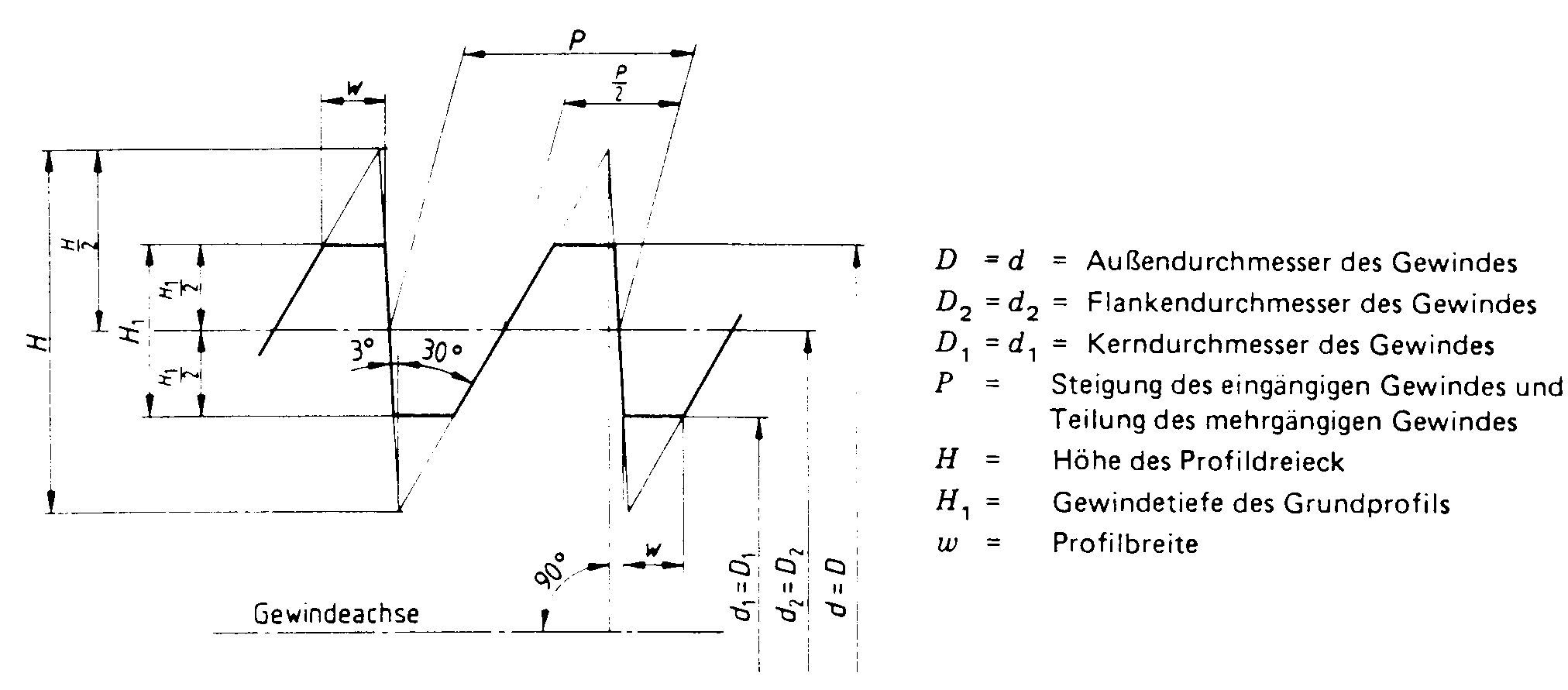
Bild 8:Grundprofil des Säegengewindes
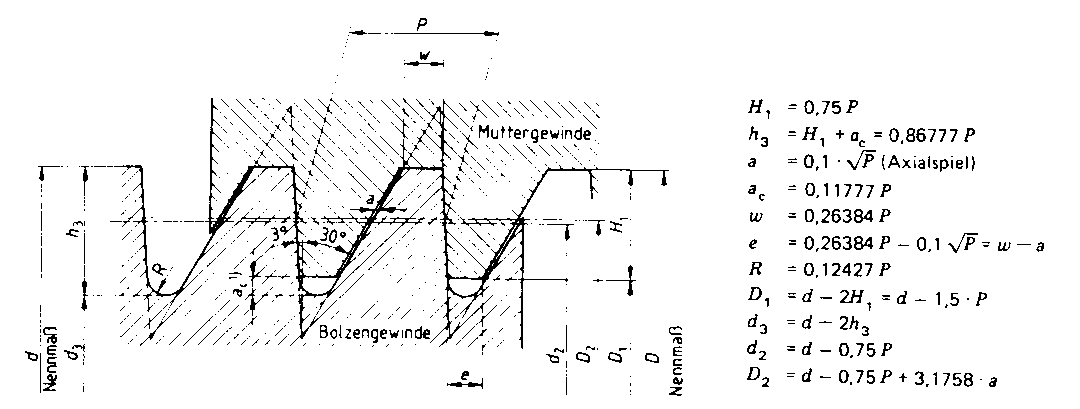
Bild 9: Profile für Bolzen-und Muttergewinde mit Spiel an den nichttragenden Flanken im Kern durchmesser und ohne Spiel zwischen den tragenden Flanken im Außendurchmesser (Nennmaße)
Die Zuordnungen der Gewindedurchmesser und Steigungen sind aus der Tabelle in DIN 513, Teil 2, Abschnitt 4 zu entnehmen.
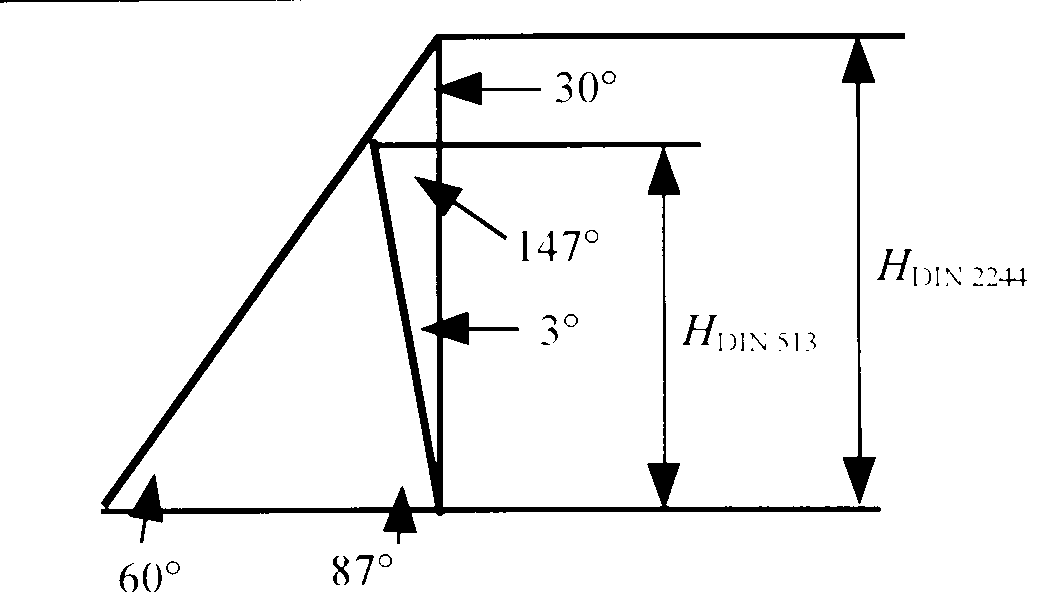
Bild 10: Ermittlung des Ersatzwinkels
Unter Berücksichtigung des Sinussatzes errechnet sich somit die Höhe des Profildreiecks zu
H = ctg 30° *sin 30°/sin 147°*cos 3° = 1,5879*P.
Zur Berechnung des Abstreifdurchmessers wird in diesem Falle ein rechnerischer Ersatzwinkel benötigt. Dieser beträgt
ctg a ersatz = ctg 30° *sin 30°/sin 147°*cos 3° = 1,5879,
somit beträgt der rechnerische Ersatzwinkel
a ersatz = 32,201°
Für die Berechnung des Abstreifdurchmesser wird, wie im Abschnitt 2.3.3 ausgeführt, der Werkstoff-Faktor a B benötigt, der sich zu
a B = t M/(t M+t B)
errechnet.
Unter Berücksichtigung des Flankendurchmessers und der rechnerischen Ersatzwinkels errechnet sich der Abstreifdurchmesser zu
dt = d2+2(0,5-a B)*P/tan 32,2°
Aus der DIN 513, Teil 1 (siehe Bild 2) geht hervor, daß die Gewindetiefe des Grundprofils H1 = 0,75P beträgt. Unter Berücksichtigung der tragenden Höhe ergibt sich als maximaler Abstreifdruchmesser
dt = d2+H1 = d2+0,75P
Da der Wert 2*(0,5-a B)*P/tan 32,2° = 0,75P ist, ist dann (0,5-a B) = 0,75*tan 32,2/2 = 0,2362 und daraus ergibt sich der maximale Werkstoff-Faktor zu
a B = 05-0,2362 = 0,2638
a M = 1-a B
für den größten Abstreifdurchmesser. Beim kleinsten Abstreifdurchmesser beträgt
a B = 1-0,2638 = 0,7362
Mit diesen Werten würden die Abstreifdurchmesser bei den Gewindespitzen des Bolzens und der Mutter liegen.
Um sicher zu stellen, daß der Abstreifdurchmesser nicht an den Spitzen der Gewindegänge liegt, sollte die Bedingung
d > dt > D1
erfüllt sein. Diese Bedingung ist dann erfüllt, wenn der Werkstoff-Faktor
a B = 0,3 bis 07
beträgt.
Die erforderliche Scherfläche des Abscherzylinders beträgt mit der Zugkraft F, errechnet aus dem Spannungsquerschnitt mit der Zugfestigkeit, bzw. Mindeststreckgrenze
At = F*(1/t M + t B)
Damit wird die Einschraubtiefe
m = At /(dt *p )
Gemäß DIN 513, Bild 2 (siehe auch Bild 9) befindet sich bei der nichttragenden Flanke ein Axialspiel von
a = 0,1*Ö P
Zum Ausgleich dieses Freimaßes, sind die Anzahl der Gewindegänge
Z = m/P
zu ermitteln. Somit ergibt sich die Länge des Ausgleichs zu
ma = Z*a = Z*0,1*Ö P
Damit wird die effektive Einschraubtiefe
meff = m+ma
Die Berechnung der in den Gewindegängen auftretenden Scherspannungen und vorhandenen Sicherheiten werden wie im Abschnitt 2.3.3 aufgeführt berechnet.
Für die Berechnung der Trapez- und Sägengewinde-Spindeln sind einige Mutternwerkstoffe der PAN-Metalle in der nachstehenden Tabelle aufgeführt.
|
PAN- Werkstoff |
Herstellungsart |
R0,2 [N/mm²] |
Rm [N/mm²] |
Härte HB 10 |
s d0,2 = pG [N/mm²] |
pmax [N/mm²] |
b M |
E-Modul [N/mm²] |
a T |
|
Bz. 10 |
G |
150 |
280 |
75 |
160 |
40 |
|
110000 |
0,0000175 |
|
|
GZ, GC |
170 |
320 |
90 |
160 |
40 |
|
110000 |
0,0000175 |
|
Bz. 12 |
G |
180 |
300 |
95 |
210 |
50 |
0,64 |
100000 |
0,0000180 |
|
|
GZ, GC |
200 |
350 |
110 |
210 |
60 |
0,64 |
100000 |
0,0000180 |
|
Bz. 14 |
G |
170 |
250 |
115 |
180 |
60 |
0,68 |
95000 |
0,0000185 |
|
|
GZ, GC |
200 |
320 |
125 |
180 |
65 |
0,68 |
95000 |
0,0000185 |
|
SoBz 16 |
G |
180 |
250 |
130 |
160 |
70 |
0,85 |
80000 |
0,0000185 |
|
|
GZ, GC |
220 |
300 |
150 |
160 |
80 |
0,85 |
80000 |
0,0000185 |
|
AlMBz. 220 |
G |
330 |
650 |
170 |
290 |
120 |
0,32 |
125000 |
0,0000170 |
|
|
GZ, GC |
380 |
750 |
180 |
290 |
150 |
0,32 |
125000 |
0,0000170 |
Anmerkung: G = Formguß, GZ = Schleuderguß, GC = Strangguß, GK = Kokillenguß
pmax = Max. Flächenpressung, bei der ein Gleiten noch möglich ist.
PAN-Metallgesellschaft Baumgärtner GmbH & Co.KG, Am Oberen Luisenpark 3, D 68165 Mannheim
Tabelle 1: PAN-Gleitmetalle
Literatur:
[1] Stückle, R. "Berechnung der Schrauben (nach
Bach)",Uhlands Ingenieur-Kalender 1939,
65. Jahrgang, Teil
II, Seite 104 und 105, Kröner Verlag Stuttgart, 1938
[2] Alexander, E.A. "Analysis and design of threaded assemblies". Int. Automotive Engng. Congress and Exposition, Detroit. 1977 Rep.-Nr.770420.
[3] Richtlinie VDI 2230, Bl. 1:Systematische Berechnung hochbeanspruchter Schraubverbindungen (Juli 1986, korregierter Nachdruck 1990)
[4] Dose, G.F.; Pittner, K.-J. "Neuartige Berechnung von Schrauben unter Berücksichtigung der Werkstoffkennwerte", Konstruktion 48 (1996), Heft 6, Seite 183 bis 188, Springer Verlag, Berlin
[5] Dose, G.F. "Ermittlung der Scherspannungsfaktoren für die neuartige Schraubenberechnung", Konstruktion 49 (1997) Heft 1/2, Seite 28 bis 32, Springer-VDI-Verlag, Düsseldorf.
[6] Dose, G.F. "Anwendung eines Schraubenberechnungs-Verfahrens auf verschiedene Gewindearten", Konstruktion 50 (1998) Heft 7/8 , Seite 45 bis 49, Springer-VDI-Verlag, Düsseldorf.
[7] Hasselmann, Uwe "Grenzflächenpressung verspannter Teile ", Vortrag zur 5. Informations- und Diskussionsveranstaltung SCHRAUBENVERBINDUNGEN - Neue Ergebnisse aus Forschung und Praxis, TU Darmstadt